Синтез рекурсивных цифровых фильтров с линейной фазой
Введение
Рекурсивная цифровая фильтрация по сравнению с нерекурсивной позволяет, как известно, обеспечивать значительно более высокое качество частотной селекции цифровых сигналов при высокой эффективности работы рекурсивного фильтра в реальном времени. Однако рекурсивные фильтры имеют, как указано во многих источниках [1–3], нелинейную фазочастотную характеристику (ФЧХ), что практически не дает возможности использовать рекурсивную цифровую фильтрацию в широком спектре задач цифровой обработки сигналов. Однако нелинейность фазы вовсе не базовое свойство рекурсивного цифрового фильтра, а является только следствием несовершенной методики его проектирования. Действительно, при косвенном проектировании рекурсивного фильтра через аналоговый прототип методом билинейного преобразования или его модификациями в MATLAB, к основным факторам, определяющим нелинейность фазы коэффициента передачи, относятся:
- Нелинейность частотной шкалы цифрового фильтра, приводящая к нелинейным искажениям как модуля, так и фазы частотного коэффициента передачи фильтра, особенно при больших углах (значениях цифровой частоты).
- Этап аппроксимации требуемой АЧХ фильтра по Чебышеву, Баттерворту или Кауэру, которая, как известно, является нелинейно-фазовой процедурой.
- Нелинейность процедуры приведения коэффициентов рекурсивного фильтра к целочисленному виду, что дополнительно искажает фазу.
Однако основной причиной фазовой нелинейности является то, что при косвенном проектировании рекурсивного фильтра через аналоговый прототип ни на одном этапе классического метода билинейного преобразования требования по фазе коэффициента передачи проектируемого фильтра не учитываются и не могут быть учтены в принципе. Фильтр проектируется лишь по требуемой амплитудно-частотной характеристике (АЧХ), то есть на максимальную селекцию цифрового сигнала по амплитуде, естественно, ценой больших фазовых искажений. Поэтому и неудивительно, что рекурсивные фильтры высокого порядка, спроектированные через аналоговый прототип, имеют нелинейность ФЧХ порядка сотен градусов. Физически это объясняется тем, что в основных формах построения (прямой и последовательной) как рекурсивный, так и нерекурсивный цифровой фильтр является дискретной минимально-фазовой системой, в которой модуль и аргумент частотного коэффициента передачи связаны преобразованием Гильберта:
А значит, нельзя независимо управлять фазой коэффициента передачи — это приведет к неизбежному изменению его модуля, то есть АЧХ фильтра. Поэтому ужесточение требований по фазе рекурсивного фильтра возможно только за счет снижения его амплитудной селективности, так как эти два показателя являются принципиально противоречивыми. Если использовать традиционную оценку селективных свойств фильтра среднеквадратичной ошибкой s выполнения требований к АЧХ фильтра:
где Yn(X) — текущее значение модуля коэффициента передачи фильтра на n‑й дискретной частоте диапазона определения, а YnT — требуемое значение частотной характеристики, то связь амплитудной селекции и фазовых искажений Dj(w) рекурсивного фильтра может быть отражена следующим образом:
s×Dj(w) ≈ const ≈ k/N,
где N — порядок рекурсивного фильтра.
Фазовые искажения при этом определяются максимальным отклонением текущей фазы фильтра от линейной:
где jL — требуемая линейная ФЧХ фильтра.
Постановка задачи дискретного синтеза
Требование фазовой линейности рекурсивной цифровой фильтрации может быть полностью выполнено при переходе к прямому синтезу рекурсивного фильтра методами дискретного математического программирования [4–8]. Общая идея математического программирования (МП) состоит в привязке решения задачи к четкому инвариантному математическому признаку — экстремуму функции качества объекта F(X), который также называют целевой функцией, где Х — вектор искомых параметров устройства. Для любой проектной задачи такую функцию в общем виде всегда можно сформировать исходя из требуемого функционирования устройства. (В компьютерных пакетах это обычно делает функциональный редактор.) Имея такую целевую функцию, решение задачи синтеза устройства сводят к процедуре минимизации F(X), то есть к определению координат глобального экстремума (оптимальных параметров устройства XО), что обычно делают с помощью поисковых методов [6–8].
Важным требованием к рекурсивному фильтру является выполнение цифровой фильтрации в реальном времени. Это означает, что все операции алгоритма фильтрации должны выполняться за время, не превышающее период дискретизации входного сигнала. С точки зрения эффективной работы цифрового фильтра в реальном времени и обеспечения минимума затрат (по времени и ресурсам памяти) для расчета отклика фильтра особый интерес представляет случай целочисленной дискретизации пространства параметров (коэффициентов) фильтра. Дело в том, что целочисленное проектное решение, безусловно, предпочтительно при аппаратной реализации рекурсивного фильтра на ПЛИС, как и на других цифровых платформах с целочисленной арифметикой вычислений.
При целочисленной дискретизации пространства параметров задача МП трансформируется в задачу целочисленного нелинейного программирования (ЦНП). Таким образом, принципиальное отличие дискретного ЦНП-синтеза заключается в том, что в данном случае для удовлетворения требуемого функционирования рекурсивного фильтра на стадии его проектирования не используются никакие искусственные приемы и подходы классических методов (аналоговые прототипы, методы аппроксимации, нормировки и квантования параметров), приводящие к существенным ограничениям в выполнении функциональных требований и систематическим ошибкам, а осуществляется прямой поиск требуемых целочисленных коэффициентов фильтра прямо по его математическому определению (рекурсивной модели).
Критерием поиска является соответствие совокупного текущего функционирования фильтра его требуемому функционированию. Формально критерий поиска определяется значением целевой функции F(IX), которую при синтезе фильтра необходимо минимизировать. Здесь уже IX — вектор целочисленных параметров (коэффициентов) проектируемого фильтра.
Для обеспечения высокой селективности и возможности реализации сложной формы характеристик целочисленный рекурсивный фильтр наиболее целесообразно проектировать в форме каскадного соединения m = N/2 рекурсивных целочисленных звеньев второго порядка [6], где N — общий порядок рекурсивного фильтра. Системная функция такого фильтра имеет следующий вид:
где комплексная переменная z = ejw, а w = (2pf)/FД — цифровая частота.
Из соотношения (3) легко получается разностное уравнение для одного звена рекурсивного целочисленного фильтра:
yn = (b0xn+b1xn–1+b2xn–2–a1yn–1–a2yn–2)/a0. (4)
При вычислении отклика фильтра необходимо выполнять операцию деления на целочисленный нормирующий коэффициент a0, которая может быть реализована операцией побитового сдвига при условии принадлежности каждого i‑го нормирующего коэффициента биномиальному целочисленному ряду:
a0i ∈ {2q}, q = 0,R–1 i = 1,m, (5)
где R — разрядность цифровой платформы.
На рис. 1 приведена структура звеньев рекурсивного целочисленного фильтра, соответствующая разностному уравнению (4). Как показано на этом рисунке, при аппаратной реализации на ПЛИС для вычисления отклика фильтра yn, кроме традиционных операций сложения, умножения и задержки на такт, есть и операция сдвига на B = log2a0 бит, с помощью которой, как уже сказано, реализуется целочисленное деление на биномиальный нормирующий коэффициент a0. Условие же устойчивости рекурсивного селективного фильтра может быть записано как
где pi — полюс передаточной функции (3) в Z‑плоскости.
При синтезе рекурсивного фильтра с линейной фазой целевая функция обычно формируется в виде аддитивной свертки двух частных целевых функций fАЧХ(IX) и fФЧХ(IX). Они обеспечивают соответственно выполнение требований как к амплитудной селекции фильтра, так и к линейности его фазы:
F(IX) = b1fАХЧ(IX)+b2fФЧХ(IX). (7)
Частная целевая функция fАЧХ(IX) при этом определяется соотношением (1), а функция fФЧХ(IX) — соотношением (2).
Относительно целевой функции (7) задача дискретного целочисленного программирования для синтеза рекурсивного фильтра в форме каскадного соединения m‑звеньев второго порядка записывается так [6]:
где R — разрядность цифровой платформы, d — индекс коэффициента передаточной функции звена второго порядка (3).
Общая экстремальная задача дискретного синтеза (8) записана относительно целочисленного пространства I6m параметров (коэффициентов фильтра), размерностью 6m. Ограничения (9) задают границы изменения этих целочисленных коэффициентов, а соотношение (10) определяет принадлежность коэффициентов a0i биномиальному ряду (5). Функциональные ограничения (11) контролируют в процессе синтеза условие устойчивости рекурсивного фильтра по всем полюсам коэффициента передачи.
Дискретный синтез рекурсивного фильтра с линейной фазой
Рассмотрим в качестве примера решение конкретной задачи многофункционального синтеза рекурсивного фильтра нижних частот четвертого порядка с полосой пропускания 0–70 кГц при усилении в полосе на уровне 1,8. Фаза коэффициента передачи должна быть максимально линейной в полосе пропускания фильтра.
Графики требуемых характеристик синтезируемого фильтра приведены на рис. 2 и 3 (они выделены красным цветом).
Задача дискретного программирования для синтеза рекурсивного ФНЧ в форме кас-кадного соединения двух звеньев второго порядка под цифровую платформу с разрядностью R = 14 записывается так:
Таким образом, минимизация целевого функционала осуществлялась на 12‑мерном целочисленном пространстве параметров в допустимой области (13) и (14) при выполнении функциональных ограничений устойчивости фильтра (15) по всем его четырем полюсам. Целевой функционал этой задачи формировался в виде аддитивной свертки (7) при одинаковой значимости требований к амплитудной селекции проектируемого фильтра и линейности его фазы (b1 = b2 = 1).
В таблице приведены найденные оптимальные значения целочисленных коэффициентов передаточной функции проектируемого фильтра. Время решения этой задачи на ЭВМ не превышало 12 минут, причем значение целевого функционала в начальной точке составляло 9100, а значение в точке оптимума было равно 0,00011, при полном выполнении условий (15) устойчивости рекурсивного фильтра.
|
Звено фильтра |
Коэффициенты передаточной функции фильтра |
|||||
|
a0 |
a1 |
a2 |
b0 |
b1 |
b2 |
|
|
1 |
8192 |
–2418 |
211 |
2864 |
–9439 |
–5422 |
|
3 |
16384 |
–10 000 |
2459 |
–4570 |
–2006 |
–3277 |
В качестве цифровой платформы для аппаратной реализации синтезированного ФНЧ была выбрана программируемая логическая схема Spartan 3AN FPGA фирмы Xilinx. Программирование осуществлялось на языке VНDL под заданную структуру фильтра (рис. 1) и найденные целочисленные коэффициенты ее звеньев.
Измерение частотных характеристик фильтра осуществляется на реальном сигнале с помощью автоматизированной панорамной измерительной системы, разработанной в среде виртуальных приборов LabVIEW. Реальные измеренные частотные характеристики фильтра для частоты дискретизации 320 кГц приведены на рис. 2 и 3.
Как видно на приведенных графиках, требования по функциональным характеристикам рекурсивного фильтра были выполнены с высокой точностью. Фазовые искажения Dj(w) в полосе пропускания фильтра не превышали трех градусов.
Таким образом, правильно спроектированный рекурсивный фильтр не может иметь нелинейную фазу. При прямом синтезе рекурсивных фильтров методами дискретного программирования техническая линейность фазы (Dj — не выше одного-трех градусов) может быть гарантирована.
Заключение
Методы целочисленного нелинейного программирования в приложении к задачам проектирования цифровых фильтров являются современной и весьма перспективной альтернативой традиционным классическим методам проектирования цифровых фильтров [1–3]. Современные алгоритмические комплексы целочисленной минимизации позволяют надежно и эффективно решать такие задачи при выполнении всех внешних требований и ограничений к работе цифрового фильтра. Это дает возможность существенно повысить качество проектируемых фильтров, сократить время их разработки и заметным образом снизить их стоимость.
По материалам, приведенным в статье, видно, что в сравнении с традиционными классическими подходами синтез цифровых фильтров методом дискретного программирования позволяет:
- Осуществлять синтез цифровых фильтров по совокупности требуемых характеристик, причем можно легко управлять приоритетом функциональных характеристик в процессе синтеза фильтра.
- Форма характеристик может быть произвольной, а частотная шкала — линейной.
- Возможна широкая фрагментация характеристик, когда важные их участки выделяются в отдельное функциональное окно для их детальной проработки в ходе синтеза.
- Устойчивость решения для рекурсивных фильтров может быть гарантирована приоритетным выполнением функциональных условий устойчивости в процессе синтеза фильтра.
- Целочисленная дискретизация пространства варьируемых параметров фильтра позволяет получать проектные решения в целых числах, что снимает все ограничения по арифметике вычислений при аппаратной реализации фильтров как на микропроцессорных контроллерах, так и на ПЛИС. Это подтверждают приведенные в статье экспериментальные данные.
Более подробно вопросы технической реализации рекурсивного ЦНП-фильтра на ПЛИС, включая сведения об использованных ресурсах ПЛИС и достигнутой тактовой частоте, будут рассмотрены в последующих публикациях.
- Антонью А. Цифровые фильтры: анализ и проектирование. Пер. с англ. М.: Радио и связь, 1983.
- Каппелини В., Константинидис А. Дж., Эмилиани П. Цифровые фильтры и их применение. М.: Энергоатомиздат, 1983.
- Баскаков С. И. Радиотехнические цепи и сигналы. М.: Высшая школа, 2005.
- Мину М. Математическое программирование. Теория и алгоритмы. М.: Наука, 1990.
- Корбут А. А., Финкельштейн Ю. Ю. Дискретное программирование. М.: Наука, 1959.
- Бугров В. Н. Проектирование цифровых фильтров методами целочисленного нелинейного программирования // Вестник ННГУ. 2009. № 6.
- Бугров В. Н., Лупов С. Ю., Земнюков Н. Е., Корокозов М. Н. Дискретный синтез цифровых рекурсивных фильтров // Вестник ННГУ. 2009. № 2.
- Воинов Б. С., Бугров В. Н., Воинов Б. Б. Информационные технологии и системы: поиск оптимальных, оригинальных и рациональных решений. М.: Наука, 2007.

 отправка...
отправка...


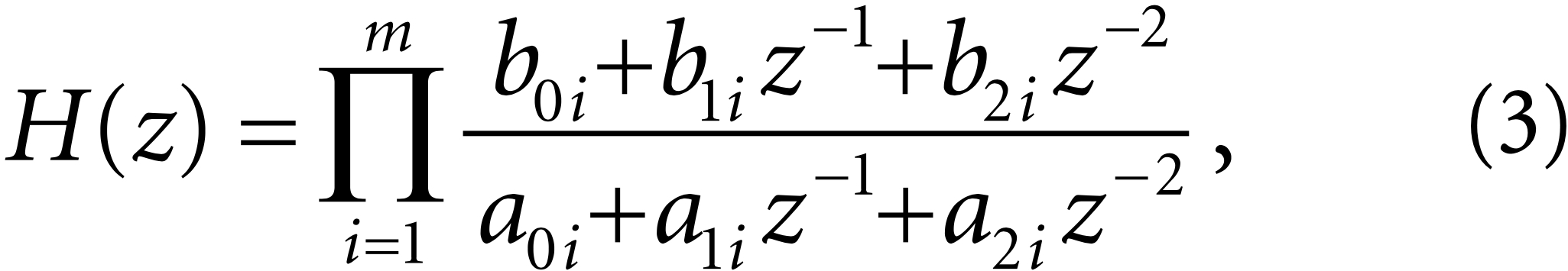


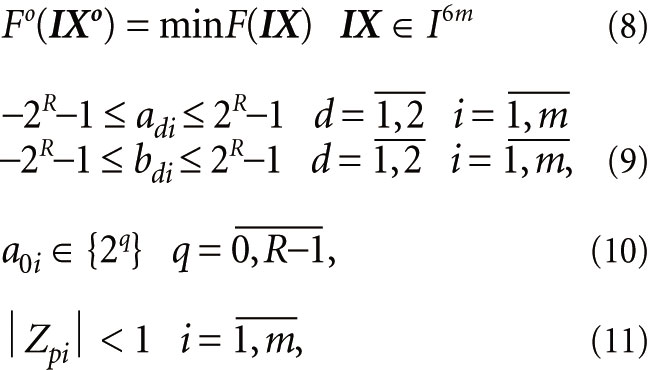



 30 июля, 2021
30 июля, 2021 6 января, 2021
6 января, 2021