Система компьютерной алгебры Mathematica 9: новые возможности

Введение

Среди существенных новинок системы Mathematica 9 следует особо отметить:

• Обновленный интерфейс (Wolfram Predictive Interface).
• Системную поддержку единиц измерений.
• Анализ социальных сетей, выживаемости и надежности.
• Случайные процессы и стохастические дифференциальные уравнения.
• Параметрические дифференциальные уравнения.
• Гибридные и дифференциально-алгебраические уравнения.
• Работу с временными рядами.
• Интеграцию с R.
• Распознавание лиц на фотографиях.

В систему Mathematica 9 были добавлены новые крупные составляющие, еще более расширяющие не имеющую себе равных базу алгоритмических, информационных возможностей и возможностей пользовательского интерфейса системы Mathematica [2, 3, 5, 6, 7]. Обеспечена тесно интегрированная поддержка более чем 4500 единиц измерений, в том числе свободная форма языкового ввода, преобразования и проверка согласования размерностей в построении графиков, в численных и символьных вычислениях (пакет расширения Units Package). Общее число функций в ядре системы выросло почти до 4000. Mathematica 9 является обратно совместимой со всеми ноутбуками (документами), созданными в версиях 6, 7 и 8.

Mathematica 9 содержит огромный набор средств статистики. Они заслуживают отдельного рассмотрения, которое (за исключением метода наименьших квадратов) не вошло в задачи этой статьи, ввиду ограниченности ее объема и специфики материала по статистике.

Mathematica 9 для компьютеров MAC

Для компьютеров MAC фирмы Apple поставляется новейшая версия Mathematica 9.01 (30.01.2013). Ее основное достоинство (помимо стандартных для этих компьютеров деталей интерфейса) — предотвращение потери быстродействия на компьютерах MAC с микропроцессорами Intel и поддержка их параллельных вычислений. На рис. 1 показан исходный интерфейс системы Mathematica 9.01. В целом это стандартный многооконный интерфейс системы Mathematica.

Рис. 1. Исходный интерфейс Mathematica 9.01 для MAC

Для тестирования Mathematica 9 на время вычислений надо выполнить комплексный тест Benchmark, содержащий 15 последовательно выполняемых тестов:

In[1]:=Needs[“Benchmarking`”]
In[2]:= Benchmark[]
Out[2]//InputForm=
{“MachineName” –> “macbook-pro-vladimir-4”,
    “System” -> “Mac OS X x86 (64-bit)”, “BenchmarkName” –> “MathematicaMark9”,
    “FullVersionNumber” –> “9.0.1”, “Date” –> “June 23, 2013”,
    “BenchmarkResult” –> 1.13, “TotalTime” –> 12.252,
    “Results” –> {{“Data Fitting”, 0.541}, {“Digits of Pi”, 0.733},
        {“Discrete Fourier Transform”, 0.927}, {“Eigenvalues of a Matrix”, 0.673},
        {“Elementary Functions”, 1.058}, {“Gamma Function”, 0.568},
        {“Large Integer Multiplication”, 0.539}, {“Matrix Arithmetic”, 1.147},
        {“Matrix Multiplication”, 0.937}, {“Matrix Transpose”, 0.84},
        {“Numerical Integration”, 0.934}, {“Polynomial Expansion”, 0.125},
        {“Random Number Sort”, 1.563}, {“Singular Value Decomposition”, 0.839},
        {“Solving a Linear System”, 0.828}}}

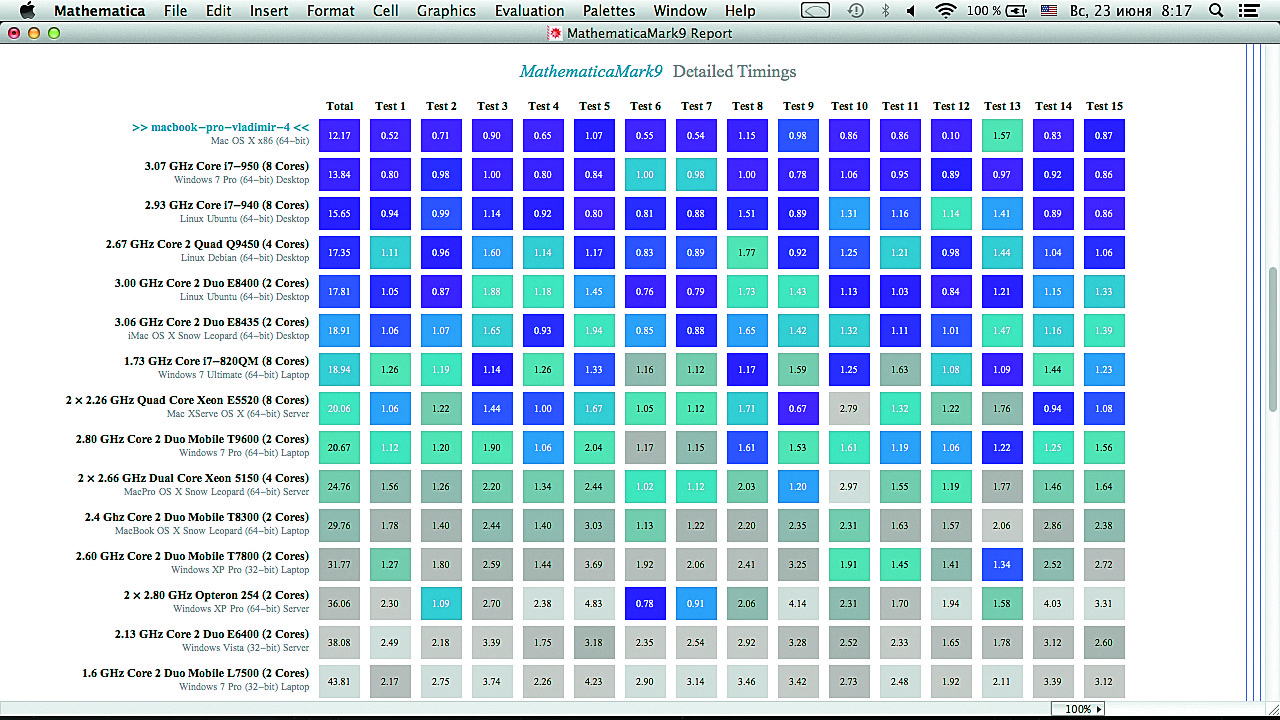
Более полный отчет о времени вычислений можно получить, исполнив команду:

In[1]:= BenchmarkReport[]

Часть расширенного отчета показана на рис. 2. Цифры в прямо-угольниках — соответствующие времена вычисления того или иного теста (перечень тестов дан в конце отчета).

Рис. 2. Часть отчета о времени вычислений в системе Mathematica 9

Новым стало окно центра документации — справки. Оно представлено на рис. 3. Центр имеет лаконичный каталог разделов, но каждый раздел раскрывается активизацией мышью треугольничка после своего названия. Раздел Get Srarted (верхняя строка) знакомит пользователя с началом работы с системой, а раздел What’s is New — с новинками системы.

Рис. 3. Окно центра документации на фоне окна командного режима с примерами применения

Ноутбук (документ) в системе Mathematica состоит из набора входных и выходных ячеек. Справа они отмечаются длинными квадратными скобками разного уровня. Входные ячейки заполняются начиная с пустого места с помощью клавиатуры, навигатора функций и палитр различных объектов (рис. 4). Палитры содержат свыше 2000 символов.

Рис. 4. Палитры символов, математических знаков и других объектов

Выходные ячейки содержат результаты выполнения входных ячеек, завершаются нажатием клавиш Shift+Enter. Нажатие просто Enter переводит строку. Следует сразу обратить внимание, что названия функций имеют одну букву, одно слово или несколько слов. Все они начинаются с большой буквы. Список параметров функций дается в квадратных скобках. Эти правила традиционны во всех версиях системы.

Информация о новых возможностях

Особенностью системы Mathematica, выгодно отличающей ее от других быстро развивающихся систем, является наличие детальной информации о новых возможностях и функциях каждой версии системы — начиная с 6.0. Это облегчает пользователю разбор ноутбуков (документов) системы вне зависимости от того, в какой версии системы они созданы.

При общем знакомстве с новыми возможностями системы удобен тематический указатель (рис. 4, слева). Окно справки из раздела New in 9 показано на рис. 5. Оно содержит подробный алфавитный каталог новинок, позволяющий быстро найти любое новое средство (например, функцию или оператор) по его имени и сразу выйти на соответствующее подробное описание.

Рис. 5. Окно с полным алфавитным каталогом новых функций Mathematica 9

Функциям в Mathematica принадлежит особое место. По существу основой системы является функциональный язык программирования в виде набора создаваемых пользователем и встроенных функций. Их применение значительно облегчает навигатор функций, который позволяет легко найти любую из многих тысяч встроенных функций и вывести ее шаблон в текущую строку ввода ноутбука (рис. 6). Решение задач обычно сводится к заданию функции в строке ввода и получению результата в строке вывода.

Рис. 6. Окно навигатора функций на фоне окна одного из разделов справки

По выбранной функции в навигаторе можно вывести окно с ее детальным описанием (рис. 7), включающим теоретическую часть, синтаксис записи, многочисленные (порою десятки) примеры применения, указания на схожие по тематике разделы справки, пакеты расширений, самоучители и т. д. С помощью мышки и треугольничков перед названиями разделов они могут открываться или закрываться.

Рис. 7. Окно справки по всем математическим функциям

Mathematica 9 для компьютеров класса PC

Для компьютеров класса PC с операционной системой Windows XP, Windows 8 и др. могут поставляться 64‑разрядная и 32‑разрядная версии Mathematica 9.0, чуть отличающиеся по скорости выполнения операций. На рис. 8 показан исходный интерфейс 32‑разрядной версии Mathematica 9.0.

Рис. 8. Исходный интерфейс 32 разрядной версии Mathematica 9 для PC

Сравнив рис. 2 и 8, нетрудно заметить, что разница в интерфейсе крайне незначительна и сводится к отличиям в титульной строке окон: в версии под MAC кнопки управления окнами цветные и круглые и расположены в начале титульной строки, а в версии для PC — квадратные и серые. Скорость выполнения операций в системах под Windows даже немного выше, чем у систем под MAC OS.

Предсказание дальнейших вычислений

Новинкой в Mathematica 9 являются средства предсказания вычислений. Как только пользователь закончил вычисления, на его рассмотрение будут представлены оптимизированные предложения, имеющиеся в специальной линейке (Suggestions Bar) и позволяющие сделать следующие возможные шаги (рис. 9). Нажатием нужной кнопки в этой линейке можно выполнить новую функцию, построить график или открыть модуль оперативной помощи. Данный подход помогает уже в начале работы ориентироваться в функциях системы Mathematica и открывать для себя новые функциональные возможности.

Рис. 9. Работа с помощью линейки предложений:
а) пример вычисления;
б) пример построения графика выражения

Например, после ряда вычислений, показанных на рис. 9а, линейка предложений предсказывает построение в первую очередь графика результата. Исполнив это предложение, получим график в виде параболы, что показано на рис. 9б. Если вычисления исчерпаны, линейка предложений исчезает.

Многие предложения обладают динамическими и интерактивными элементами управления, позволяя задать нужные значения и увидеть результаты, прежде чем пользователь остановит свой выбор на одном из них.

О совместимости версий Mathematica

Последние версии Mathematica стали появляться так часто, что в употреблении одновременно находится несколько версий системы. Если, к примеру, пользователь привык работать с версией Mathematica 6.0 [2, 3], ему нет смысла переходить на новейшую версию Mathematica 9 без весьма серьезных оснований. В частности, таким основанием может быть отсутствие нужных средств в старой версии. Поэтому встает вопрос о совместимости новейшей версии системы с предшествующими версиями.

Wolfram Research всегда уделяла решению этого вопроса большое внимание. Автор проходил длительную стажировку на фирме Wolfram Research еще в 2000 году, когда там велась интенсивная разработка Mathematica 5. Уже тогда ему были показаны многие средства, которые в последующие годы вошли в серийные продукты Mathematica 6, 7 и 8 [2, 3, 5, 6, 7], а затем и в Mathematica 9. Этот огромный задел теперь используется в невиданной по масштабам и темпам модернизации системе.

Если ноутбук выполнен в старой версии, то об этом появляется сообщение и предложение конвертировать выражение в подходящую форму. Даже если проводится обновление с версии 5.2 или еще более ранней версии 5.0, можно работать с такими ноутбуками в Mathematica 9 (при условии, что есть необходимые наборы шрифтов, в частности кириллических).

Предварительный обзор графики в справке

Практика показывает, что при знакомстве со справкой системы особый интерес у пользователя вызывают примеры с графической визуализацией вычислений. В прежних версиях Mathematica найти такие примеры среди многих тысяч, представленных в справке, было довольно трудно. В Mathematica 9 этот вопрос решен: в начале каждого заслуживающего внимания раздела справки приведен небольшой набор графиков, наглядно иллюстрирующих типовые средства визуализации демонстрационных примеров данного раздела (рис. 10).

Рис. 10. Окно справки по разделу языка программирования микропроцессора

На рис. 11 показан один из примеров построения контурных графиков поля потоков, полученных таким образом.

Рис. 11. Контурные графики поля потоков

Пакеты расширения

Ядро системы оптимизировано по числу входящих в него заранее откомпилированных функций. Поэтому часть функций в Mathematica включена в ее пакеты расширения, которые надо открывать перед использованием таких функций. Скажем, при работе с размерными величинами следует открыть пакет Units с помощью команды:

<< Units`

Теперь можно пользоваться размерными величинами:

In[1]:= Convert[12 Meter/Second, Mile/Hour]
Out[1]= (37500 Mile)/(1397 Hour)
In[2]:= SI[3 Atmosphere]
Out[2]= 303975. Pascal
In[3]:= ConvertTemperature[20, Fahrenheit, Centigrade]
Out[3]= –(20/3)

Описание всех пакетов расширения есть на сайте фирмы [1]. В формате PDF-файлов оно бесплатное. Их можно также заказать и купить в виде книг. Переход компьютеров на новую элементную базу, в частности многоядерные процессоры, позволил сократить число пакетов расширения, а их функции включить в состав откомпилированного ядра системы, без заметной потери на загрузку ядра и поиск в нем нужных данных.

Средства динамической интерактивности

Начиная с Mathematica 6 в систему введены новые мощные средства динамической интерактивности. Они достаточно подробно описаны в [2, 3] и полностью доступны в Mathematica 9. В них входит большое число управляющих объектов. Это однокоординатные и двухкоординатные слайдеры, локаторы, списки, меню, таблицы и т. д., обычно управляемые мышью. Есть ряд модулей, ограничивающих динамическую интерактивность своим пространством. Например, модуль манипуляций

Manipulate[expr, {u, min,max, du}]

позволяющий манипулировать объектом expr при изменении управляющей переменной u от значения min до значения max с шагом du. При этом объект будет динамически менять свой вид при действиях с управляющими объектами вручную или автоматически.

Средства динамической интерактивности используются при численных и аналитических расчетах. Рис. 12а иллюстрирует их применение при численных расчетах совместно с управляющим объектом — однокоординатным слайдером.

Рис. 12. Динамическая интерактивность:
а) при численных расчетах;
б) при вычислении неопределенных интегралов

Применение этих средств при аналитических расчетах (при вычислении неопределенных интегралов одной группы) показано на рис. 12б. Нетрудно заметить, что интегралы, как и другие специальные математические знаки, могут задаваться из палитр в естественном математическом виде, а могут задаваться своими символьными именами — например, Integrate для интегрирования.

Примеры графики с динамической интерактивностью

Динамическая интерактивность особенно полезна, когда в результате решения надо получить наглядную визуализацию результатов вычислений в динамике. Примером может служить построение спиралей, проходящих через заданные точки на плоскости, перемещаемые мышью в любое место (рис. 13). Такие точки задает на плоскости управляющий элемент — локатор. В программу он вводит координаты точки — своего центра с перекрестием.

Рис. 13. Построение спиралей, проходящих через заданные точки, перемещаемые мышью

Другой наглядный пример — построение стилизованной фигуры человека, изображения рук и ножек которого могут вращаться мышью (рис. 14). Такое вращение можно задать и в автоматическом режиме, активизировав маленькие круглые кнопки с крестиками. Этот пример демонстрирует также применение функций построения объектов графики — отрезка прямой (Line) и диска (Disk).

Рис. 14. Построение стилизованной фигуры человека с конечностями — линиями, перемещаемыми слайдерами

При описании многих преобразований синусоидальных сигналов, например при их кодоимпульсной фазовой манипуляции, широко применяемой в скоростных цифровых линиях связи, их удобно представлять как проекции вращаемого мышью радиус-вектора. Рисунок 15 иллюстрирует построение такого радиус-вектора и построение в виде красной точки проекции его конца. Вращая радиус-вектор мышью, можно наблюдать перемещение точки в то или иное положение. На построении совокупности таких точек основано создание «звездных» диаграмм в современных цифровых осциллографах и анализаторах спектра.

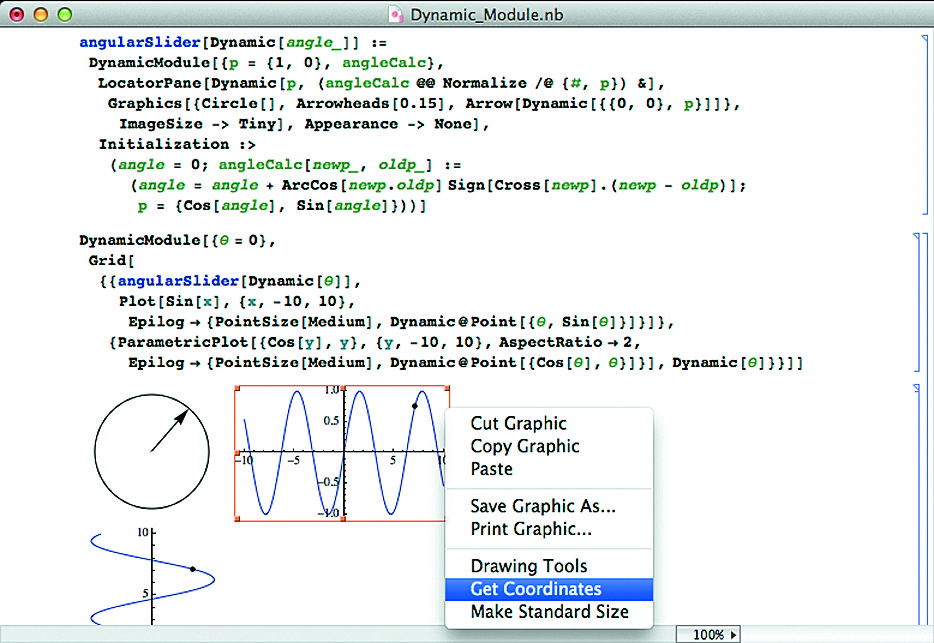
Рис. 15. Построение радиус-вектора синусоиды, его вращение мышью и нахождение места конца на проекциях синусоиды

Другой пример (рис. 16) обеспечивает построение фигур Лиссажу, которые обычно формируются довольно дорогими приборами — осциллографами. Их построение в Mathematica не только более наглядно, но и дает устойчивые фигуры. Управление обеспечивается слайдерами.

Рис. 16. Построение фигур Лиссажу с управлением двухкоординатными слайдерами

На практике широко применяется полиномиальная аппроксимация заданных на плоскости точек. Рисунок 17 дает пример такой аппроксимации для точек, перемещаемых мышью с помощью локаторов. Линия аппроксимации почти мгновенно проходит точно через эти точки. Порядок полинома устанавливается однокоординатным слайдером. Проведение аппроксимации очень наглядно и позволяет оценивать основные ее закономерности.

Рис. 17. Полиномиальная аппроксимация перемещаемых мышью точек с установкой слайдером порядка полинома

Построение контурного графика поля двух перемещаемых на плоскости точек показано на рис. 18. Для построения таких точек используются слайдеры и локаторы. Следует обратить внимание на выбор типа цветовой закраски областей между кривыми.

Рис. 18. Контурный график поля двух перемещающихся мышью точек

Динамическую интерактивность можно использовать для наблюдения плавного перехода (трансформации) одной кривой или фигуры в другую. На рис. 19 это показано на примере трехмерной фигуры при изменении параметра «a». Он меняется слайдером.

Рис. 19. Трансформация поверхности в пространстве

Рисунок 20 показывает построение трехмерной фигуры Knot с выбором пары параметров из таблицы. Отчетливо видно высокое качество имитации освещения фигуры и ее окраски. Размеры окна графики, как и в других примерах, в широких пределах можно менять мышью.

Рис. 20. Построение трехмерной фигуры Knot с разными параметрами

Анимация при графической визуализации

Анимация — это еще один пример динамической интерактивности. Она реализуется функцией:

Animate[expr,{u,umin,umax,du}]

Есть ее более простые и более сложные формы синтаксиса. Объект expr анимирует при изменении управляющей переменной u от u_min до u_max с шагом du.

На рис. 21а даны примеры анимации символьного выражения и графики. Управляющий параметр изменяется однокоординатным слайдером каждого рисунка.

Рис. 21. Примеры анимации:
а) символьного выражения и двумерного графика;
б) параболы, сопровождаемой звуком

Звук также может быть объектом анимации. На рис. 21б показан пример анимации графика параболы, сопровождаемой анимацией звука с помощью встроенного проигрывателя звуковых файлов. Разумеется, для этого компьютер должен иметь звуковую карту и звуковые колонки (телефоны).

Некоторые другие возможности графики

Динамическая интерактивность возможна и при построении более сложных графиков. На рис. 22а изображено построение циферблатов действующих (и показывающих реальное время) часов, расположенных на гранях куба. Сам куб при этом может с помощью мыши поворачиваться в пространстве.

Рис. 22. Построение:
а) идущих часов на гранях управляемого мышью куба;
б) трехмерных фигур и поверхности с применением модуля динамики

Построение семейства трехмерных фигур и поверхности представлено на рис. 22б. Здесь при построении использован модуль DynamicModule, ограничивающий своими пределами область динамической интерактивности.

На рис. 23 показано изменение цвета кривой графика с помощью слайдера внутри панели выбора цвета с применением динамической интерактивности. Выбранный цвет указан и в маленьком прямоугольнике ячейки ввода.

Рис. 23. Выбор цвета кривой графика

Построение ряда трехмерных фигур с разной окраской показано на рис. 24. Используется таблица фигур и обычная техника построения фигур.

Рис. 24. Таблицы трехмерных фигур с разным стилем окраски при отражении света

Решение задач математического анализа

Решение задач математического анализа — одно из важнейших предназначений системы Mathematica и достаточно подробно описано в [2, 3], так что ограничимся несколькими примерами.

Для упрощения математических выражений используется функция Simplify. Она работает с алгебраическими и тригонометрическими выражениями и с элементарными функциями. Пример работы с алгебраическим выражением:

In[1]:= D[Integrate[1/(x^3 + 1), x], x]
Out[1]= 1/(3 (1 + x)) – (–1 + 2 x)/(6 (1 – x + x^2)) + 2/(3 (1 + 1/3 (–1 + 2 x)^2))
In[2]:= Simplify[%]
Out[2]= 1/(1 + x^3)

Функция FulSimplify обеспечивает работу и с выражениями, содержащими специальные функции:

In[1]:= FullSimplify[x Gamma[x]]
Out[1]= Gamma[1 + x]
In[2]:= FullSimplify[E^(EllipticF[x, 1]), –Pi/2 < x < Pi/2]
Out[2]= Sec[x] + Tan[x]
In[3]:= FullSimplify[EulerPhi[p^2] + p, Element[p, Primes]]
Out[3]= p^2

Естественно, есть такие широко распространенные функции компьютерной алгебры, как расширение выражений Expand, факторизация Factor, решение обычных уравнений и систем Solve и др. Примеры применения функции Solve:

In[1]:= Solve[x^2 + a x + 1 == 0, x]
Out[1]= {{x –> 1/2 (–a – Sqrt[–4 + a^2])}, {x –> 1/2 (–a + Sqrt[–4 + a^2])}}
In[2]:= Solve[(x^5 – 1)^x == 0, x]
Out[2]= {{x –> 1}, {x –> (–1)^(2/5)}, {x –> –(–1)^(3/5)}}
In[3]:= Solve[AiryBi[1 – x^2] == 0 && 2 < x < 3, x, Reals]
Out[3]= {{x –> Sqrt[1 – AiryBiZero[2]]}, {x –> Sqrt[1 – AiryBiZero[3]]}, {x –> Sqrt[ 1 – AiryBiZero[4]]}, {x –> Sqrt[1 – AiryBiZero[5]]}}

При необходимости решения задач в численном виде используется функция NSolve. Матрицы в Mathematica 9 задаются построчно в фигурных скобках. Затем строки объединяются с применением разделительных запятых. Приведем примеры составления и решения системы из двух линейных уравнений в символьном и численном виде:

In[1]:= LinearSolve[{{a, b}, {c, d}}, {x, y}]
{(d x – b y)/(–b c + a d), (c x – a y)/(b c – a d)}
In[7]:= m = {{1, 1, 1}, {1, 2, 3}, {1, 4, 9}};
b = {1, 2, 3};
LinearSolve[m, b]
Out[9]= {–(1/2), 2, –(1/2)}

Примеры вычисления неопределенных и определенных интегралов с помощью функции Integrate представлены на рис. 25. Исходный интеграл можно задавать в различных форматах, в том числе с помощью шаблона с естественным математическим видом интеграла. Система Mathematica 9 способна вычислять огромное число интегралов и производных и вполне может заменить детальные справочники по интегральному и дифференциальному исчислению.

Рис. 25. Примеры вычисления интегралов

Разложение функций и выражений в ряд Тейлора с помощью функции Series получается очень наглядным при использовании средств анимации (рис. 26). При этом хорошо видно, как кривая разложения отходит от графической зависимости разлагаемой функции. Параметром анимации является степень разложения полинома Тейлора.

Рис. 26. Разложение синусоиды в ряд Тейлора с анимацией

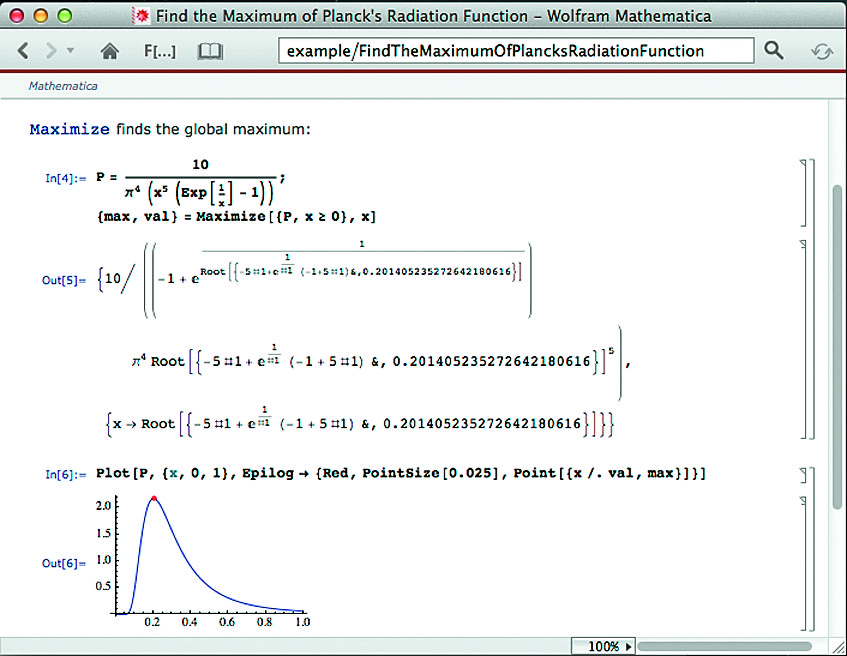
Исследование функций и уравнений составляет важную часть математического анализа. Mathematica 9 позволяет решать большое число классов уравнений и анализировать практически любые функциональные зависимости. На рис. 27, в частности, показано построение графика функции, вычислен ее максимум, и красная точка максимума построена на графике функции.

Рис. 27. Вычисление максимума функции с построением точки максимума

Часто требуется приблизить некоторую совокупность точек с ошибками некоторой кривой, проходящей в «облаке точек», с наименьшей среднеквадратической погрешностью (то есть реализовать метод наименьших квадратов). Основной функцией, реализующей это, является функция FindFit. Пример приближения точек двумя кривыми со сравнением результатов показан на рис. 28.

Рис. 28. Сравнение случаев приближения точек кривой по методу наименьших квадратов

В центре документации можно найти огромное число примеров решения и других задач математического анализа.

Решение дифференциальных уравнений

В Mathematica 9 существенно расширены и модернизированы средства решения дифференциальных уравнений — как в символьной, так и в численной форме. Приведем примеры решения в символьной форме с применением функции решения дифференциальных уравнений и систем с ними Dsolve:

In[4]:= DSolve[y′[x] + y[x] == a Cos[x], y[x], x]
Out[4]= {{y[x] –> E^-x C[1] + 1/2 a (Cos[x] + Sin[x])}}
In[5]:= DSolve[{y′[x] + y[x] == a Cos[x], y[0] == 1}, y, x]
Out[5]= {{y –> Function[{x}, 1/2 E^–x (2 – a + a E^x Cos[x] + a E^x Sin[x])]}}
In[6]:= DSolve[y″[x] + 4 y′[x] + 5 y[x] == 0, y[x], x]
Out[6]= {{y[x] –> E^(–2 x) C[2] Cos[x] + E^(–2 x) C[1] Sin[x]}}

Для численного решения предназначена функция NDSolve. Решения получаются более наглядными при использовании динамической интерактивности (рис. 29). Для этого применяется специальный решатель уравнений Equation Trekker, позволяющий мышью задать начальную точку решения в виде фазового портрета. Его окно показано под ноутбуком. По завершении работы решение появляется как строка вывода ноутбука.

Рис. 29. Построение решения дифференциального уравнения с выбором начальной и конечной точки решения мышью

Часто требуется не одно решение, а целое семейство, получаемое при изменении какого-либо параметра (рис. 30а). Это позволяет по густоте линий решения оценивать его чувствительность к изменению заданного параметра.

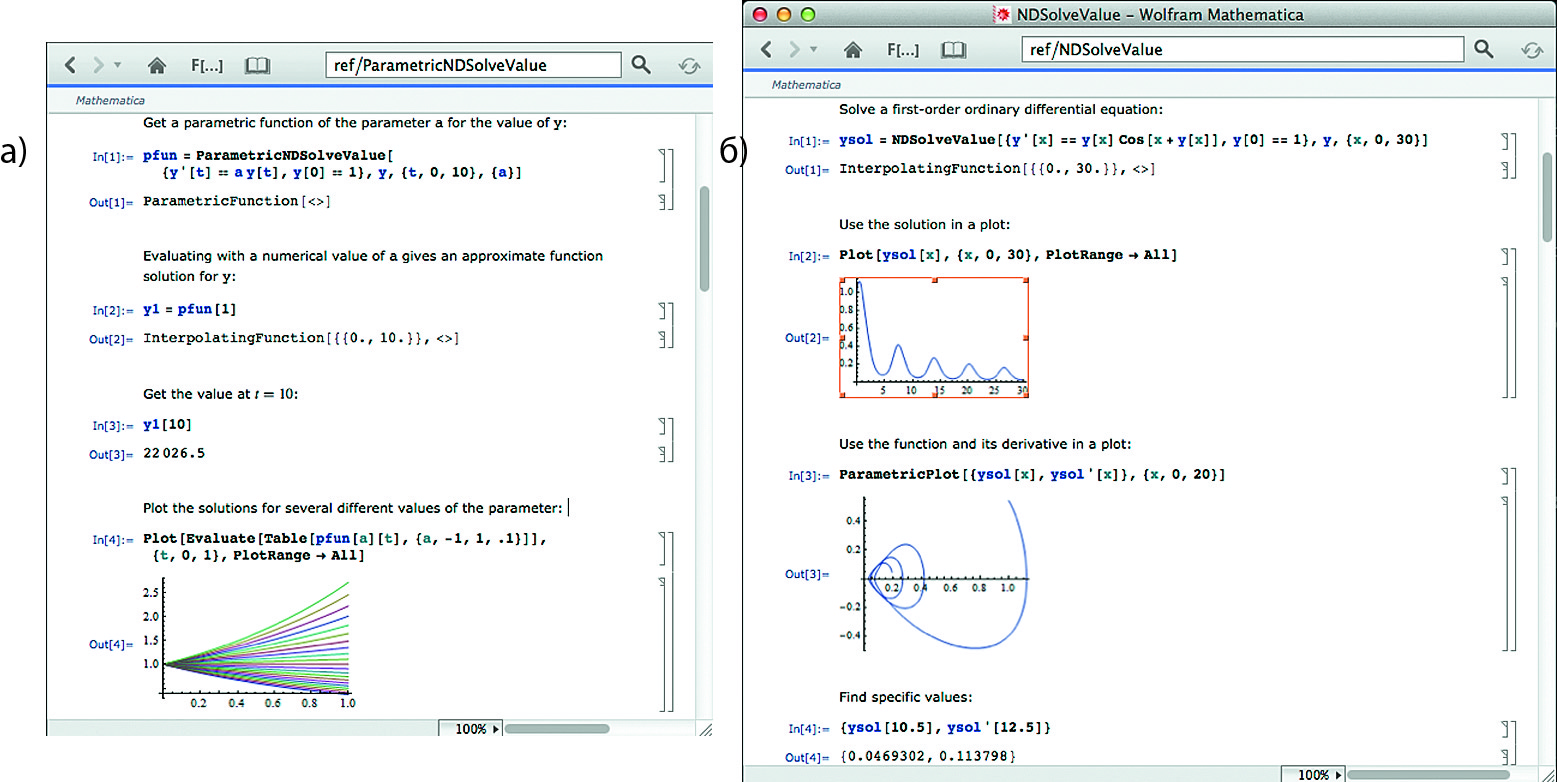
Рис. 30. Решение дифференциального уравнения с построением:
а) семейства графиков решений;
б) графика решения и фазового портрета

При решении систем дифференциальных уравнений низкого порядка график решения часто отображается с помощью параметрических фигур — фазовых портретов. Пример такого решения с построением фазового портрета показан на рис. 30б.

Моделирование на основе решения жестких дифференциальных уравнений

Решение дифференциальных уравнений часто лежит в основе моделирования динамических систем и устройств. Многие из них описываются нелинейными дифференциальными уравнениями (часто специального типа), не имеющими аналитических решений. В этом случае применяются численные методы. В Mathematica 9 средства для работы с дифференциальными уравнениями существенно расширены. В частности, введены эффективные методы решения жестких дифференциальных уравнений численными методами.

На рис. 31 показан пример решения системы жестких дифференциальных уравнений Ван-дер-Поля. Решения имеют как медленные, так и быстрые участки, что указывает на большую разницу в постоянных времени решения. Эта классическая нелинейная система из двух дифференциальных уравнений первого порядка описывает колебания в ряде электронных схем LC-генераторов. При большом значении параметра нелинейности (1000 в нашем случае) система уравнений становится жесткой, и ее решение обычными методами невозможно. В нашем случае применен stif-метод для решения системы Ван-дер-Поля и получено решение в виде фазового портрета.

Рис. 31. Решение системы жестких дифференциальных уравнений Ван-дер-Поля с построением фазового портрета

К жестким системам относятся дифференциальные уравнения химической кинетики. Начало решения одной из таких систем показано на рис. 32а. Конец с результатами решения дан на рис. 32б.

Рис. 32. Система дифференциальных уравнений химического реактора:
а) задание;
б) решение

Решение проблемы двухсторонних граничных условий

Иногда нужно лишь то решение дифференциального уравнения, при котором соблюдаются заданные не только начальные, но и конечные граничные условия. Пример — стрельба по цели с заданными координатами. В Mathematica есть средства для решения подобных уравнений и без динамической интерактивности. Пример дан на рис. 33.

Рис. 33. Решение дифференциального уравнения с двухсторонними граничными условиями

Решение системы дифференциальных уравнений с событиями

В некоторых случаях в ходе решения дифференциальных уравнений или систем могут происходить события (events), которые надо выделять, например цветом. Mathematica 9 имеет средства и для таких «экзотических» уравнений. На рис. 34 показано решение системы дифференциальных уравнений, имеющих отрезки дуг с целочисленными значениями. Они и выделяются цветом.

Рис. 34. Решение системы дифференциальных уравнений с событиями

Моделирование двухфазного выпрямителя

Двухфазный диодный выпрямитель (rectifier), работающий на емкостную нагрузку, — одна из самых распространенных схем (рис. 35а). Он применяется едва ли не в каждом источнике питания от промышленной сети переменного тока.

Рис. 35. Моделирование двухфазного выпрямителя с емкостным фильтром:
а) начало;
б) конец

Выпрямитель также описывается жесткими дифференциальными уравнениями, поскольку при открытых диодах постоянная времени заряда конденсатора фильтра мала, а при закрытых диодах постоянная времени разряда конденсатора велика. Как видно из рис. 35б, это не препятствует моделированию в системе Mathematica 9.

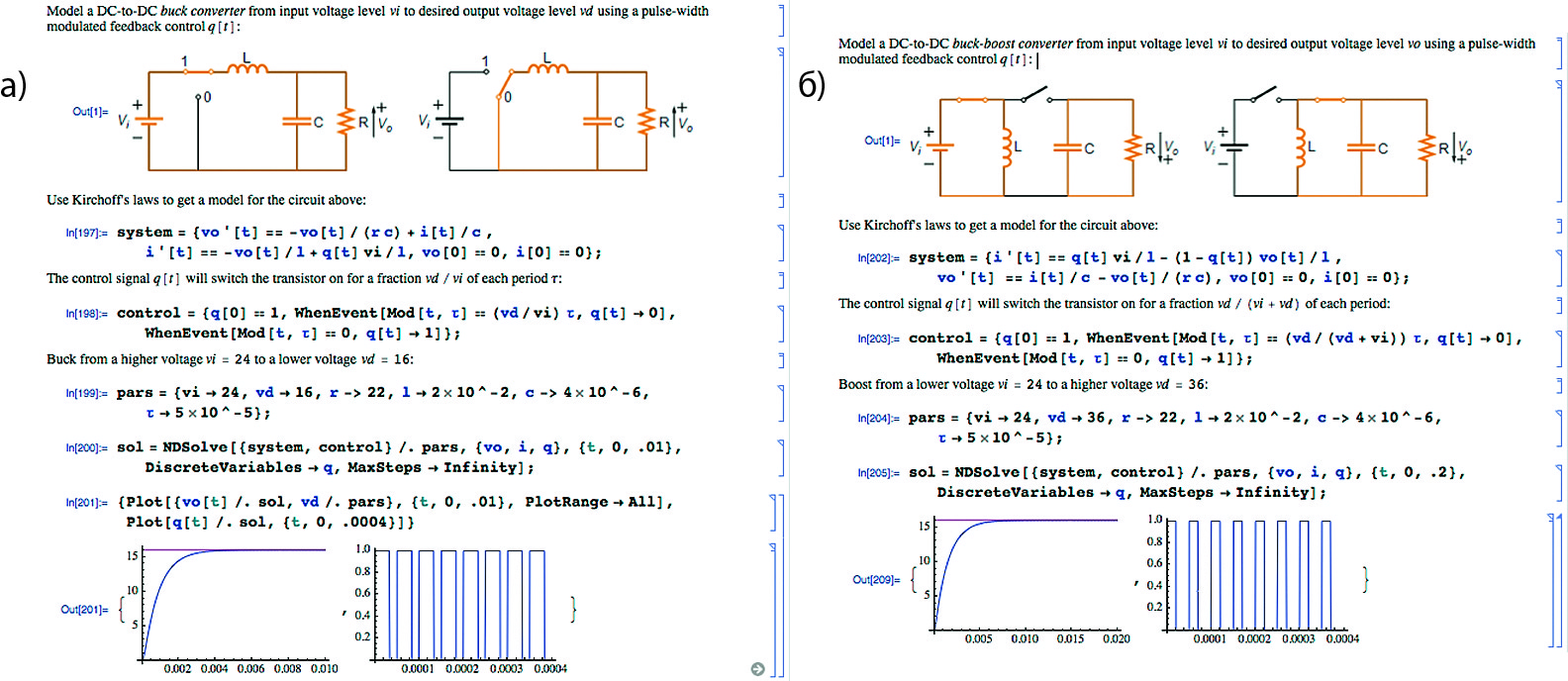
Функциональное моделирование DC/DC-преобразователей

Решение дифференциальных уравнений для функций с событиями расширяет возможности Mathematica 9 и позволяет (в основном на функциональном уровне) моделировать DC/DC-преобразователи ключевого типа. Два примера моделирования представлены на рис. 36.

Рис. 36. Моделирование обратноходового DC/DC-преобразователя:
а) тип 1;
б) тип 2

Обе схемы преобразователей построены на основе идеальных ключей, управляемых с постоянной частотой и скважностью 2.
Для открытого и закрытого состояния ключей составляется своя эквивалентная схема. Они стыкуются при решении систем дифференциальных уравнений схемы. Расчетные переходные характеристики и управляющие сигналы представлены на графиках.

Заключение

Хотя система компьютерной алгебры Mathematica 9 была создана менее чем через год после появления предшествующей версии системы, она основательно доработана и дополнена четырьмя сотнями новых объектов — в основном функций. При этом она вобрала все средства и функции более ранних версий системы Mathematica. В результате общее число функций в системе достигает примерно 4000. В справке системы содержатся многие тысячи демонстрационных примеров. Масштабы доработки систем Mathematica беспрецедентны и превосходят работы по совершенствованию конкурирующих с ними систем компьютерной алгебры Maple.